sibrtye sivrceSi

ganvixiloT pirveli rigis gantoleba sami ucnobiT

A sadac (1)

Aanu AA,B,C koeficientebidan erTi mainc aranulovania.

Teorema. Nnebismieri sibrtye sivrceSi marTkuTxa koordinatTa sistemaSi moicema (1) gantolebiT da piriqiT, nebismieri aseTi gantoleba marTkuTxa koordinatTa sistemaSi aRwers sibrtyes.

Ddamtkiceba. marTlac vTqvaT π sibrtye mocemulia Tavisi wertiliT da n aranulovani normaluri veqtoriT. MmaSin sivrce sam nawilad gaiyofa: erTi nawili sibrtyis wertilebia, danarCeni ori nawili ki sibrtyis sxvadasxva mxares mdebare wertilebisgan Sedgeba. is Tu am sami nawilidan sad mdebareobs sivrcis nebismieri M wertili ganisazRvreba skalaruli namravlis n niSniT. kerZod:

Tu M wertili π sibrtyeze mdebareobs maSin n =0 radgan kuTxe n da veqtorebs Soris marTia. Tu es M wertili π sibrtyeze ar mdebareobs maSin es kuTxe maxvilia da n >0, an blagvia da n <0. Aam skalaruli namravlis niSani sibrtyis erT mxares mdebare wertilebiTvis erTnairia.

avRniSnoT koordinatebi: , , MmaSin = da Tu M wertili π sibrtyeze mdebareobs gvaqvs:

,

Aanu frCxilebis gaxsniT gvaqvs:

, sadac .

aq A,B,C koeficientebidan erTi mainc aranulovania, radgan veqtori aranulovania. amiT damtkicda Teoremis pirveli nawili, e.i. rom sibrtye aris (1) gantolebis geometriuli saxe.

Teoremis meore nawilis dasamtkiceblad avirCioT ricxvebi , ,

, romlebic akmayofileben (1) gantolebas. (aseTi ricxvebi arsebobs, mag. Tu SegviZlia aviRoT , =). am ricxvebs Seesabameba wertili , romelic ekuTvnis (1) gantolebis geometriul saxes. Gvaqvs

(2)

gamovakloT (1)-s (2), miviRebT

(3)

(3) toloba aris orTogonulobis kriteriumi veqtorebisTvis (A,B,C) da , sadac wertili M es kriteriumi sruldeba im sibrtyis wertilebisTvis romelic gadis wertilze da (A,B,C) veqtoris marTobulia (da ar sruldeba sivrcis sxva wertilebisTvis.) e.i. (1) aris aRniSnuli sibrtyis gantoleba. ▄

GgansazRvreba. A(1) gantolebas ewodeba sibrtyis zogadi gantoleba. Kkoeficientebs A,B,C aqvs geometriuli azri: veqtori n=(A,B,C) sibrtyis marTobulia, amitom mas ewodeba sibrtyis normaluri veqtori.

sibrtyis specialuri saxis gantolebebi.

Eesenia:

1. sibrtyis veqtoruli da parametruli gantolebebi;

2. sam mocemul wertilze gamavali sibrtyis gantoleba;

3. sibtyis gantoleba monakveTebSi;

4. sibrtyis normaluri gantoleba;

1. vTqvaT da da wertilebis radius veqtorebia. MmaSin

= da piroba rom sibrtye gadis wertilze da veqtoris marTobulia SegviZlia CavweroT skalaruli namravlis gamoyenebiT (anu da veqtorebis skalaruli namravli nulis tolia)

0, (4)

n

0

(4) gantolebas ewodeba sibrtyis veqtoruli gantoleba.

Ffiqsirebul sibrtyeze (sivrceSi) avirCioT ori aranulovani da arakolinearuli veqtori, anu bazisi (gavixsenoT bazisi).

Aanu arsebobs ricxvebi , rom

=,

Aanu . (5)

(5) gantolebas ewodeba sibrtyis parametruli gantoleba, parametrebiT ,

sam mocemul wertilze , , , gamavali sibrtyis gantolebaa

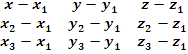= 0 . (6)

Ddamtkiceba. Uunda vaCvenoT rom am sam mocemul wertilze gamaval sibrtyeze mdebare M=(x,y,z) wertilebis simravle moicema (6) gantolebiT.

(6) niSnavs rom sami veqtoris Sereuli namravli nulia:

kerZod am sami veqtoris koordinatebia determinantis striqonebi, anu:

;

da

veqtorebia Sereuli namravli nulia,

es ki aris am sami veqtoris komplanarobis (anu erT sibrtyeze mdebareobis) kriteriumi. anu es aris kriteriumi M, , , , wertilebis erT sibrtyeze yofnis. r.d.g.

SevniSnoT rom Tu (6)-s gavSliT pirveli striqonis mixedviT gveqneba

_ () + ()=0

(7).

Dda frCxilebis gaxsnis mere miviRebT sibrtyis zogad gantolebas.

(7)-Si meore rigis dererminantebi aris da

veqtorebis veqtoruli namravlis koordinatebi. Ees veqtoruli namravli orive veqtoris da amitom maTze gamavali sibrtyis marTobulia; e.i. sibrtyis normaluri veqtoria da misi gamoCena sibrtyis zogad gantolebaSi didi siurprizi araa.

sibtyis gantoleba monakveTebSi

vTqvaT sibrtye sakoordinto RerZebze CamoWris monakveTebs a,b,c, maSin misi gantolebaa

+ + = 1 (8).

Ddamtkiceba. Ees sibrtye gadis wertilebze

gamoviyenoT (6):

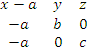= 0,

Aanu

bc(x-a)+ acy+abz=0;

gavyoT abc da gavamartivoT, miviRebT (8).