SERGO
TOPURIA
(To the 80th Birthday Anniversary)

This year Professor Sergo Topuria, Honored Scientist, Doctor of Physical and
Mathematical Sciences, would have been 80 years old and marked 55 years of his
scientific and pedagogical activities. He was a prominent Georgian
mathematician, a remarkable
representative of the Georgian mathematical school, an excellent teacher and
educator. He was one of those Georgian mathematicians who in the 60s of the past
century made the first bold steps in mathematical research and thereby won
general recognition and respect.
Sergo Topuria was born on December 27, 1931 and died this year, on March 15th.
He was a person with lofty ideals and adhered to high moral and civic
principles. His path in life, high professional competence and general public
recognition are an evidence of his faithful service to the country and people.
The
results obtained by S. Topuria reflect the onward development of the studies
carried out by such famous mathematicians as B. Luzin, I. Privalov, A. Zygmund,
G. Hardy, I. Marcinkiewisz, I. Stein, V. Shapiro, E. Gobson and others. He was
deeply respected and his scientific works were highly appreciated by modern
well-known mathematicians S. Nikolski, P. Ulyanov, S. Stechkin, N.
Muskhelishvili, I. Vekua and others.
In
1953, Sergo Topuria graduated with honors the physical and mathematical faculty
of Sukhumi Pedagogical Institute and continued his education as a post-graduate
student under the supervision of well-known Georgian mathematician,
Corresponding Member of the Georgian Academy of Sciences, Professor Vladimer
Chelidze. In 1959, he defended his Master’s thesis “On Some Tauber Type Theorems
for Multiple Series and Multiple Integrals”at A. Razmadze Mathematical Institute
of the Georgian Academy of Sciences.
In
1960, Sergo Topuria was elected head of the higher mathematics and theoretical
mechanics chair of the Georgian Subtropical Agriculture Institute in the city of
Sukhumi. In 1966, he moved to Tbilisi and took up work as docent at higher
mathematics chair no. 3 at Georgian Polytechnical Institute. From 1967 to the
last day of his life he headed higher mathematics chair no. 63 at the
above-mentioned institute, which later was reorganized into Georgian Technical
University. Due to his outstanding organizational capacity and strenuous
efforts, in the course of many years this chair had been one of the leading
chairs of Georgian Technical University. Concurrently, for many years he was
delivering a special course of lectures for students of the
mechanical-and-mathematical faculty of I. Javakhishvili Tbilisi State
University. Along with teaching, organizational and social activities, he
carried out scientific research with enthusiasm typical of him and, in 1973, he
defended his Ph.D. thesis on the topic “Some Problems of the Boundary Properties
of Harmonic Functions, the Theory of Fourier-Laplace and Fourier multiple
trigonometric series”.
In
1975, the title of professor was conferred on Sergo Topuria and, in 1978, the
title of an Honored Scientist.
Sergo Topuria was known as a highly skilled specialist in the function theory.
Comprehensive studies were carried out by him in multidimensional harmonic
analysis. His scientific results are related to the following main directions:
summability of multiple trigonometric series for various types of convergence;
Tauber type theorems for multiple series and integrals; summation of Fourier-Laplace
and differentiated Fourier-Laplace series by the linear method; representation
of various measurable and almost everywhere finite functions of many variables
by multiple trigonometric series and Laplace series; the boundary properties of
harmonic functions in multidimensional domains.
Sergo Topuria established an analogue of S. Bernstein’s inequality for a
spherical polynomial in the space Lp(S3), 1
< p < ¥.
Sergo Topuria carried out a detailed study of the question of summability of
Fourier-Laplace series and their differentiated series (in terms of various
types of convergence). In particular, he proved analogues of the theorems of P.
Siolini, I. Stein and G. Sunuochi on almost everywhere convergence of the Cesaro
means 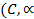 )
of Fourier_laplace series for a critical exponent.
)
of Fourier_laplace series for a critical exponent.
Furthermore, he proved the theorems on the summability in the sense of the Abel
and 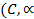 )
methods of Fourier-Laplace series and their differentiated series in the case
where the angular part of the Laplace operator written in polar coordinates is
used as a differentiation operator. He also obtained the analogues of the
theorems of G. Riesz and I. Stein on convergence the metric of a space of Cesaro
means for a critical exponent when 1 < p <
¥. He also studied the question of
strong summability of Fourier-Laplace series. Here he obtained the theorems
which are specific analogues of the Hardy-Littlewood , Marcinkiewicz and Stein
theorems.
)
methods of Fourier-Laplace series and their differentiated series in the case
where the angular part of the Laplace operator written in polar coordinates is
used as a differentiation operator. He also obtained the analogues of the
theorems of G. Riesz and I. Stein on convergence the metric of a space of Cesaro
means for a critical exponent when 1 < p <
¥. He also studied the question of
strong summability of Fourier-Laplace series. Here he obtained the theorems
which are specific analogues of the Hardy-Littlewood , Marcinkiewicz and Stein
theorems.
S.
Topuria established that if f(x) is a measurable and a.e.finite function defined
on the spherical surface, then there exists a Laplace series which is summable
almost everywhere to a function f(x) by the A* method
as well as by the Rudin-Riemann method (this is an analogue of Luzin’s theorem).
S.
Topuria obtained quite a number of results related to the boundary properties of
the differentiated Poisson integral for various domains (circle, ball,
half-plane, half-space, bicylinder) and its application. He solved the Dirichlet
problem for the ball and the half-space in the case where a boundary function is
measurable and finite a.e., i.e. in a completely general case, and also he
proved the existence of an angular boundary value of a harmonic function with
the so-called B property in the ball.
S.
Topuria was the author of over 100 scientific works, including 3 monographs.
Over 30 manuals and hand-books were written by him and published under his
supervision, of which the higher mathematics manual in 5 volumes is especially
noteworthy. These volumes make up a complete course on higher mathematics (the
theory and a collection of problems). Mention should also be made of the manual
in 2 volumes for university entrants. This two-volume manual has already run
through 5 editions, has remained very popular for nearly 30 years and is
successfully used in senior classes in secondary schools.
S.
Topuria’s scientific papers and manuals are distinguished by a simple and clear
presentation of facts and ideas, refined argumentation, a multitude of original
examples and counter-examples – these qualities produce a favorable impression
on readers.
Vladimer Khocholava
List of Sergo Topuria
Scientific Works
- Topuria
S.B., On a certain generalization of Knopp theorem. Soobshch.
Akad. Nauk Gruz.
SSR, ХIХ, 4 (1957), 385-392 (in Russian).
- Topuria
S.B., On some Tauber-type theorems for double series. Soobshch.
Akad. Nauk Gruz.
SSR, ХХ, 2 (1958), 129-136 (in Russian).
- Topuria
S.B., On some Tauber-type theorems for double series and twice integrals.
Sukh. State Pedagog. Inst, Х-ХI (1958), с. 485-528 (in Russian).
- Topuria
S.B., Tauber-type theorems for Voronov methods. Sukh. State Pedagog.
Inst, ХII (1959), 177-180 (in Russian).
- Topuria
S.B., On (BP,
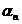 )
–summability of series, Sukh. State Pedagog. Inst., ХII (1959),
181-183 (in Russian).
)
–summability of series, Sukh. State Pedagog. Inst., ХII (1959),
181-183 (in Russian).
- Topuria
S.B., On
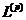 -summability
of series. Trudy GISE, V-VI (1961), 453-458
(in Russian).
-summability
of series. Trudy GISE, V-VI (1961), 453-458
(in Russian).
- Topuria
S.B.,
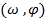 -
integrability. Trudy GISE, V-VI (1961),
459-462 (in Russian).
-
integrability. Trudy GISE, V-VI (1961),
459-462 (in Russian).
- Topuria
S.B., On summability of Fourier-Lebesgue series by
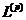 and
Voronov methods. Soobshch. Akad.
Nauk Gruz. SSR, ХХХII-3 (1963), 513-519
(in Russian).
and
Voronov methods. Soobshch. Akad.
Nauk Gruz. SSR, ХХХII-3 (1963), 513-519
(in Russian).
- Topuria
S.B., Singular double integrals and summability of Fourier integrals.
Trudy GISE, VII-VIII (1963), 377-384 (in Russian).
- Topuria
S.B., On L(p,q)-summability of double numerical series. Trudy
GISE, VII-VIII
(1963), 385-396 (in Russian).
- Topuria
S.B., On Fourier double lacunar series. Soobshch.
Akad. Nauk Gruz.
SSR, ХХХIII, 1 (1964), 9-14 (in Russian).
- Topuria
S.B., On singular and Fourier integrals. Trudy I and II resp. conf. mat.
vis., Ucheb. zav. GSSR (1964), 121-130 (in Russian).
- Topuria
S.B., Singular double integrals extending on infinite regions. Soobshch.
Akad. Nauk Gruz.
SSR, ХХХVII, 3 (1965),
513-520 (in Russian).
- Topuria
S.B., On summability of Fourier-Lebesgue double series. Soobshch.
Akad. Nauk Gruz.
SSR, ХХХVIII, 1 (1965),
7-13 (in Russian).
- Topuria
S.B., Оn the linear
methods of Summation of Fourier-Laplace series.
Soobshch. Akad. Nauk Gruz. SSR, 40, N 1, (1965), 11-18 (in
Russian).
- Topuria
S.B., On summability of Fourier-Laplace series and approximation of
functions. Trudy GISE VIII-IX (1965), 467-480 (in Russian).
- Topuria
S.B., On linear methods of summability of Fourier-Stilties multiple series.
Trudy TGU, vol. 117 (1966), 179-196 (in Russian).
- Topuria
S.B., Boundary properties of harmonic functions inside the unit sphere.
Soobshch. Akad. Nauk Gruz. SSR, 41, № 2 (1966), 265-272 (in Russian).
- Topuria
S.B., On the existence of angular boundary Values of harmonic functions in a
ball. Soobshch. Akad. Nauk Gruz. SSR, 42, № 3, (1966), 521-527 (in
Russian).
- Topuria
S.B., Summation of the
Founrier-Laplace series.
Trudy Gruz. Polytechn. Inst., N3 (115),
(1967), 7-22 (in Russian).
- Topuria
S.B., Approximation of functions by Vallee-Poussin’s sums.
Trudy Gruz. Polytechn. Inst., N6 (118),
(1967), 3-6 (in Russian).
- Topuria
S.B., On summability of double series and Fourier integrals. Тrudy
Gruz. Polytechn. Inst., N3 (123), (1968),
12-27 (in Russian).
- Topuria
S.B., Summation by Abel’s method of the differentiated Fourier-Laplace
series. Soobshch. Akad. Nauk Gruz. SSR, 54: I, (1969), 29-32 (in
Russian).
- Topuria
S.B., A general solution of the Dirichlet problem for a ball. Soobshch.
Akad. Nauk Gruz. SSR, 55:1, (1969), 25-28 (in Russian).
- Topuria
S.B.,
Classes
of
functions
and the Fourier-Laplace series.
Trudy Gruz. Polytechn.
Inst.,
N5
(133) (1969), 19-32 (in Russian).
- Topuria
S.B., Оn local boundary
properties of harmonic functions in a ball. Trudy
Gruz. Polytechn. Inst.,
N5 (133), (1969), 33-37 (in Russian).
- Topuria
S.B., Approximation of
functions by polynomials in spherical harmonics.
Trans. ХV Sci.-Techn. Conf. of Georgian Polytechn. Inst.,
2 (1970), 97-103 (in Russian).
- Topuria
S.B., On a compactness condition in some spaces and on V.A. Steklov
functions. Trudy Gruz.
Polytechn. inst.
3(138), (1970), 36-46 (in Russian).
- Topuria
S.B., Solution of the
Dirichlet problem for a half-space. Dokl.
Acad. Nauk SSSR, 195:3, (1970), 567-569 (in Russian).
- Topuria
S.B., On one property of
functions of two variables and multiple Fourier series.
Dokl. Acad. Nauk SSSR,
195:5 (1970), 1046-1049 (in Russian).
- Topuria
S.B., Summation by
Abel’s method of the differentiated Fourier-Laplace series
II. Trudy
Gruz. Polytechn. Inst.
7 (147), (1971), 17-24 (in Russian).
- Topuria
S.B., Оn the representation of functions defined on the surface of a unit
sphere by singular integrals and summability of Laplace series.
Trudy Gruz. Polytechn.
Inst., 7(147), (1971), 25-58 (in Russian).
- Topuria
S.B., Summation by Abel’s method of the differentiated Fourier series.
Dokl. Akad. Nauk SSSR,
209: 3 (1973), 569-572 (in Russian).
- Topuria
S.B., Оn one method of summation of double Fourier series. Soobshch.
Akad. Nauk Gruz.
SSR, 76:2 (1974), 289-292 (in Russian).
- Topuria
S.B., Boundary propertiers of the differentiated Poisson integral in a
circle. Trudy Gruz. Polytechn. Inst., 176:3
(1975), 13-20 (in Russian).
- Topuria
S.B., The boundary
properties of the differentiated Poisson integral in a bicylinder.
Trudy Gruz. Polytechn. Inst.,
176:3 (1975), 21-32 (in Russian).
- Topuria
S.B., The boundary properties of the differentiated Poisson integral in a
half-plane. Soobshch. Akad.
Nauk Gruz. SSR., 78:2 (1975), 281-284
(in Russian).
- Topuria
S.B., Оn the representation of functions defined on a Surface of unit sphere
by Laplace series. Soobshch. Akad.
Nauk Gruz. SSR, 82:2 (1976), 301-303 (in Russian).
- Topuria
S.B., The boundary properties of the differentiated Poisson integral, and
solution of the Dirichlet problem in a half-space.
Trudy Gruz. Polytechn. Inst., 197:6
(1977), 11-30 (in Russian).
-
Zhizhiashvili L.V., Topuria S.B., Fourier-Laplace series on the sphere.
Coll. Works “Math. Analiz” 15 (Itogi Nauki and Tehn. VINITI Akad. Nauk
SSSR), M., (1977), 83-130 (in Russian).
- Topuria
S.B., Majoranta of some singular integrals. Trudy Tbiliss. Cos. Univ.
197 (1978), 40-53 (in Russian).
- Topuria
S.B., Оn lacunary Fourier-Laplace series on the sphere. Dep. in VINITI
N79001319, 1980 (in Russian).
- Topuria
S.B., Оn the representation of dunctions of several variables by
trigonometric series. Trudy Gruz. Polytechn. Inst.,
Math. Analiz, 5(237), (1981), 9-11 (in
Russian).
- Topuria
S.B., Тugushi T.I.,
Оn The
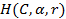 and
and
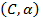 summability
of Fourier-Laplace series of functions from class L2(Sk),
summability
of Fourier-Laplace series of functions from class L2(Sk),
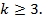 Trudy
Gruz. Polytechn. Inst. Math. Analiz.,
5(237), (1981) 12-18 (in Russian).
Trudy
Gruz. Polytechn. Inst. Math. Analiz.,
5(237), (1981) 12-18 (in Russian).
- Topuria
S.B., Some properties of the Vallee-Poussion integral on the sphere.
Trudy Gruz. Polytechn. Inst.
Math. Analiz., 3(260) (1983), 5-12 (in Russian).
- Topuria
S.B., Оn the summability
of Fourier-Laplace series on the sphere. Construct.
theory of func. 84, Sofia (1984), 81-85 (in Russian).
- Topuria
S.B., Macharashvili N.D., Sufficient conditions for the conference of
Fourier-Laplace series of a function from class L2(Sk),
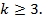 Trudy
Gruz. Polytechn. Inst., Math. Analiz, 3(285), (1985), 5-9 (in
Russian).
Trudy
Gruz. Polytechn. Inst., Math. Analiz, 3(285), (1985), 5-9 (in
Russian).
- Topuria
S.B., Summation by Abel’s method of the differentiated Fourier-Laplace
series. Trudy Gruz. Polytechn. Inst., Math. Analiz,
314:2 (1987),13-20 (in Russian).
- Topuria
S.B., Khocholava V.V., Summability of the Fourier-Laplace series by the
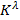 methods.
Trudy Gruz. Polytechn. Inst., Math. Analiz,
314:2 (1987), 20-32 (in Russian).
methods.
Trudy Gruz. Polytechn. Inst., Math. Analiz,
314:2 (1987), 20-32 (in Russian).
- Topuria
S.B., The Fourier-Laplace series on a sphere. Izdat. Tbilisi. TGU,
(1987), 1-356 (in Russian).
- Topuria
S.B.,
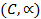 -summability
of Fourier-Laplace series in L(Sk) and almost everywhere.
Soobshch. Akad. Nauk
Gruz. SSR,134:2 (1989), 253-256 (in Russian).
-summability
of Fourier-Laplace series in L(Sk) and almost everywhere.
Soobshch. Akad. Nauk
Gruz. SSR,134:2 (1989), 253-256 (in Russian).
- Topuria
S.B., On
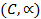 -summability
of Fourier-Laplace series on the sphere. Trudy Gruz.
Polytechn. Inst., Math. Analiz,
350:7 (1989), 5-29 (in Russian).
-summability
of Fourier-Laplace series on the sphere. Trudy Gruz.
Polytechn. Inst., Math. Analiz,
350:7 (1989), 5-29 (in Russian).
- Topuria
S.B., The boundary
properties of the differentiated Poisson integral in a half-space, and
representation of a function of two variables.
Soobshch. Akad. Nauk
Gruz. SSR, 152:2 (1995), 235-238 (in Russian).
- Topuria
S.B., The boundary
properties of derivatives of the Poisson integral in a half-space.
Soobshch. Akad.
Nauk Gruz. SSR, 152:3 (1995), 453-457
(in Russian).
- Topuria
S.B., Chikobava N.,
Summability of the Fourier series over generalized spherical
functions by the linear methods. Trudy Gruz.
Polytechn. Inst., 407:2 (1995), 155-164 (in Russian).
- Topuria
S.B., Generalized
derivatives and boundary properties of differentiated Poisson integrals for
a disk and a half-plane. Bull. Georgian Acad. Sci. 153
(1996), no. 3, 329—332.
- Topuria
S.B., Chikobava
N., Summability of the Fourier series over generalized spherical
functions by the Abel and
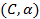 methods.
Bull. Georgian Acad. Sci. 154 (1996), no. 1,
48--51.
methods.
Bull. Georgian Acad. Sci. 154 (1996), no. 1,
48--51.
- Topuria
S.B., Macharashvili N.D.,
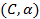 -summability
in Lp(S3) and almost everywhere of the Fourier
series over generalized spherical functions. Trudy
Gruz. Polytechn. Inst.,
Math. Analiz., 413:2 (1997), 9-17 (in Russian).
-summability
in Lp(S3) and almost everywhere of the Fourier
series over generalized spherical functions. Trudy
Gruz. Polytechn. Inst.,
Math. Analiz., 413:2 (1997), 9-17 (in Russian).
- Topuria
S.B., The boundary
properties of derivatives of the Poisson integral in a half-space,
and reprasentation of a function of two variables.
Dokl. Akad. Nauk 353:3 (1997), 306-309 (in
Russian).
- Topuria
S.B.,
Macharashvili N., On
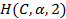 and
and
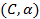 summability
of Fourier series over generalized spherical functions of
summability
of Fourier series over generalized spherical functions of 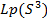 class
functions. Bull. Georgian Acad. Sci. 155 (1997),
no. 1, 14--18
class
functions. Bull. Georgian Acad. Sci. 155 (1997),
no. 1, 14--18
- Topuria
S.B., Generalized
Laplacian and boundary properties of differentiated Poisson integrals for a
half-space. Bull. Georgian Acad. Sci. 155 (1997),
no. 2, 164—167.
- Topuria
S.B., Boundary
properties of first-order partial derivatives of the Poisson integral for
the half-space
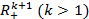 .
Georgian Math. J. 4 (1997), no. 6, 585—600.
.
Georgian Math. J. 4 (1997), no. 6, 585—600.
- Topuria
S.B., Generalized
partial derivatives of functions of many variables and boundary value
problems. Bull. Georgian Acad. Sci. 155 (1997),
no. 3, 324--327.
- Topuria
S.B., Generalized total
differentials of many variable functions and boundary value problems.
Bull. Georgian Acad. Sci. 156 (1997), no. 1, 22—26
- Topuria
S.B., Generalized
spherical derivatives and boundary value problems. Bull. Georgian Acad.
Sci. 156 (1997), no. 2, 181--184.
- Topuria
S.B., Boundary
properties of second-order partial derivatives of the Poisson integral for a
half-space
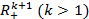 .
Georgian Math. J. 5 (1998), no. 4, 385--400
.
Georgian Math. J. 5 (1998), no. 4, 385--400
- Topuria
S.B., Generalized
derivatives and boundary properties of derivatives of the Poisson integral
for a half-space
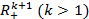 .
(Russian). Analysis Mathematica, 25,1, 1999, Budapest, 69-86.
.
(Russian). Analysis Mathematica, 25,1, 1999, Budapest, 69-86.
- Topuria
S.B., The generalized
Laplace operator on a sphere and summation of differentiated Fourier-Laplace
series using the Abel's method. Bull. Georgian Acad. Sci.
160 (1999), no. 3, 409--412 (2000).
- Topuria
S.B., The generalized
Laplace operators in the space Rk (
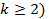 and
on the unit sphere. Trudy Gruz. Techn. Univ., 430:2 (2000), 9-18 (in
Russian).
and
on the unit sphere. Trudy Gruz. Techn. Univ., 430:2 (2000), 9-18 (in
Russian).
- Topuria
S.B., Generalized
derivatives of an arbitrary order and the boundary properties of
differentiated Poisson integrals for the half-space
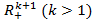 .
Georgian Math. J. 7 (2000), no. 2, 387—400
.
Georgian Math. J. 7 (2000), no. 2, 387—400
- Topuria
S.B., Boundary
properties and applications of the differentiated Poisson integral for
different domains. Tbilisi, Izdat. Gruz. Techn.
Univ., (2003), 1-236 (in Russian).
- Topuria
S.B., The generalized
Laplace operators on a unit sphere. Bull. Georgian Natl. Acad. Sci.
173 (2006), no. 1, 11—13
- Topuria
S.B., The boundary
properties of the differentiated conjugate Poisson-Stiltjes integral.
Trudy Gruz. Techn. Univ.,
460:2 (2006), 92-95
(in Russian).
- Topuria
S.B., Boundary
properties and applications of the differentiated Poisson integral for
different domains. Mathematics Research Developments Series. Nova
Science Publishers, Inc., New York, 2009. x+180 pp. ISBN:
978-1-60692-704-5.
-
Topuria S. B., Khocholava V. V.,
Mean convergence of Cesaro
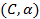 -mean
Fourier-Laplace series. Georgian Int. J. Sci. Technol. 2
(2010), no. 3, 237--241.
-mean
Fourier-Laplace series. Georgian Int. J. Sci. Technol. 2
(2010), no. 3, 237--241.
-
Topuria S. B., Macharashvili N. D.,
Lebesgue constants for
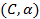 -
summation of Fourier series over generalized spherical functions.
Georgian Int. J. Sci. Technol. 2 (2010), no. 3,
297--303
-
summation of Fourier series over generalized spherical functions.
Georgian Int. J. Sci. Technol. 2 (2010), no. 3,
297--303
-
Topuria S.B., Macharashvili N.,
Tsiklauri Z., On the classes of functions and the Abelian sums of
Fourier series in generalized spherical functions. Georgian
Int. J. Sci. Technol. 2 (2010), no. 4,
![]() )
of Fourier_laplace series for a critical exponent.
)
of Fourier_laplace series for a critical exponent.![]() )
methods of Fourier-Laplace series and their differentiated series in the case
where the angular part of the Laplace operator written in polar coordinates is
used as a differentiation operator. He also obtained the analogues of the
theorems of G. Riesz and I. Stein on convergence the metric of a space of Cesaro
means for a critical exponent when 1 < p <
¥. He also studied the question of
strong summability of Fourier-Laplace series. Here he obtained the theorems
which are specific analogues of the Hardy-Littlewood , Marcinkiewicz and Stein
theorems.
)
methods of Fourier-Laplace series and their differentiated series in the case
where the angular part of the Laplace operator written in polar coordinates is
used as a differentiation operator. He also obtained the analogues of the
theorems of G. Riesz and I. Stein on convergence the metric of a space of Cesaro
means for a critical exponent when 1 < p <
¥. He also studied the question of
strong summability of Fourier-Laplace series. Here he obtained the theorems
which are specific analogues of the Hardy-Littlewood , Marcinkiewicz and Stein
theorems.